The difference between linear and exponential growth must be absolutely clear to understand our money system and its impact on our lives. Any growth by a percentage is exponential. When we talk about a 3 percent annual growth rate for our economy, we are talking about exponential growth. When we talk about a steady rate of increase in our money supply, we are talking about exponential growth.
LINEAR
Linear growth happens when you add. If you put $100 in a savings account this year and add $100 every year, at the end of 50 years, you would have $5,000 in your savings account. If you saved for 100 years, you would have $10,000. This is linear growth. You use addition, and, in this case, add a fixed amount.
EXPONENTIAL
Exponential growth happens when you multiply. If you put $100 in a savings account today and grow your savings at a rate of 10 percent each year, at the end of 50 years, you will have $11,739. If you saved at this rate for 100 years, you would have $1,378,061. This is exponential growth. You use multiplication, and, in this case, multiply by the percentage to get the amount of increase.
(I have four kids, and I always felt the first three added a linear increase in the amount of activity. The fourth child seemed an exponential increase!)
There is a wonderful Indian folktale, One Grain of Rice, about a young girl who earns a reward from a stingy Rajah. She asks for a reward of one grain of rice on the first day, and double the amount of rice from the previous day for 30 days total. The Rajah says yes, thinking she’s not asking for much. After all, it will only be two grains of rice, then four grains, then eight…what a silly girl! By the 30th day of doubling, it takes 536,870,912 grains of rice to make the day’s payment. Over the 30 days, the girl has received more than a billion grains of rice – all of the Rajah’s stores!
Humans are often focused on the present, and exponential growth can lull us to sleep with its slow growth beginning. This is such an important concept, here is another look at exponential growth in a closed system:
Imagine a lake, larger than the eye can see. On one side of the lake a traveler drops a tiny algae cell into the lake. When these algae cover a surface of water, they block the sun and kill the fish beneath. But this is a very tiny spore in a very big lake.
The algae reproduce rapidly, doubling in size every day – a 100% growth rate. If you live on this side of the lake, you might see a tiny spot of algae and then a growing expanse. If you live on the other side of the lake, you won’t see any threat at all.
The algae continue to double. Some of the people on the algae side of the lake get more and more agitated as they see the growing spread of algae, which is destroying the fish habitat in the water it covers. A few, who know their math, are nearly hysterical and waving Save the Fish signs. The people on the other side of the lake are wondering what all the fuss is about.
Many on both sides of the lake note that it is a big lake and the algae are only taking up a fraction of the surface.
One day, the algae cover half of the lake surface. People look out and say, “Hmm, looks like we’ve got a growing problem. We will have to act soon. Maybe we should set up a commission to study it.” Others point out the algae only cover half the lake, and it would cost too much money to do anything about it, and surely some enterprising entrepreneur will step in and fix it. The next day, the lake is covered and all the fish die.
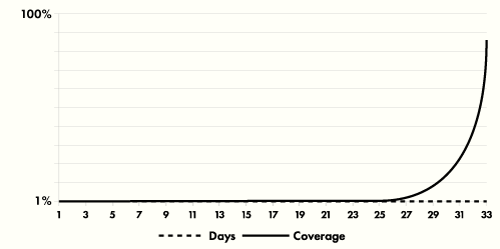
NO living system on planet earth can sustain exponential growth. This is an immutable fact. All living systems have checks that maintain balance. The only living things that grow exponentially and unchecked (for a time), such as bacteria and cancer cells, kill their hosts and then die. The question for us: will we recognize the threat our money system presents and take action in time?
Bending the curve
In real life, living systems do not grow or change with mathematical precision. There are too many variables and too many unexpected impacts. Perhaps when the traveler dropped the single spore into the water, he told someone these algae are edible and rich in nutrients; they can be harvested and a beneficial crop for your community – a great business opportunity!
However, they find it is not worth harvesting until it has grown to a substantial size, and there is only a modest demand for the algae, so the harvesting reduces the growth rate from 100% – doubling every day – to a growth rate of about 75 percent. We have added an interest group that wants to keep the algae growing because it creates jobs and makes them a profit.
Shaving off a bit of the growth rate stretches out the exponential curve but does not change the fact that if the algae continue to grow by a steady percentage each year, they will cover the lake – a little later, rather than sooner, but inevitably. That’s the math. Hanging onto the jobs now can kill all the food and jobs later.
Our brains are shaped to see the immediate and not the underlying inevitability. So, you can easily imagine lots of arguments about what caused the “sudden catastrophic increase” in the algae growth.
Deceptively slow
Hold the image of an exponential curve; the slow, almost flat beginning, the gentle swing upward, then the nearly vertical line off the chart. At first exponential growth appears deceptively slow, manageable and even something to celebrate… until it’s not.
